節洋傘を経由する球欠の体積 いた偏弧環を円錐台に加えた 「膨らんだ円錐台」 (右の上図) の体積を求めた。私は特に上が閉じた形を直観的に洋傘と呼ぶ。 これは関が9 と呼んだ立体に相当し、 これに中錐に相当する 体積を加えれば球欠の体積が得られる(1)積分: 以下の問題を考えます。 問題 なぜ、半径 r の球の体積Vは、 体積V=(4π/3) r 3 なのか。 この問題は、以下の様に解くことができます。 先に、 半径 r の球の表面積Sは、 表面積S=4π r 2 であることを求めておきます。球の体積の公式 (Vは球の体積。πは円周率。rは球の半径) 球の体積の証明 球の中心を通るx軸を想定して計算。球をそのx軸に直角に切る円の面積を積分するという考え方。その円の半径はx軸の変数xと球の半径rから三平方の定理で算出。
体積を求める
球 体積 求め方 積分
球 体積 求め方 積分- 下記の記事で、\(n\)次元空間の半径\(R\)の球の体積というのを求めました。 前回の記事はこちら n次元空間における半径Rの球の体積 ↑結果はこちらです。 せっかくなので、2次元、3次元、4次元、5次元の球の体積球の体積、表面積 中学生にも納得のいく方法で。 積分でも出します 球の体積、表面積 中学生にも納得のいく方法で。 積分でも出し




球の表面積 体積 身勝手な主張
球冠,球帯の面積の求め方01 一点から発せられた光をあるnaを持つ対物レンズで取り込む,そのときにnaによってどの程度の明るさが異なるか,など気になりますね. いろいろなサイトに,naと明るさの関係の記述があります(オリンパス).体積を数値積分で求めることを考えてみましょう。ここでは球の体積を求めること を考えます。 まず、 高校の数学3の復習です。平面に半径1の円を描き、 それをx軸もしくはy 軸について回転させれば、半径1の球が出来上がります。したがって、この性質を 断面積、積分区間を調べたら、あとは体積の積分公式に当てはめるだけです。 解答 半円を \(y = \sqrt{a^2 − x^2}\) とおき、\(\mathrm{Q}(x, 0)\) とする。
313 体積の計算 次314 曲面積上3 多重積分前312 演習問題 ~ 多重積分の積分変数の変換 313体積の計算 例 363(球の体積) 半径 の球の体積は である. これを多重積分で求める. (その 1) 球を 8 等分し底面が であり,上面が の体積 として求める.2 次元の極座標 , とおくと,領域 と等価な領域球座標の座標曲線に沿う線積分の求め方について説明しよう そのために, 例としてr 曲 線に沿う線積分を考える ベクトル場V は球座標の成分をもちいて V = Vr(r,θ,φ)er Vθ(r,θ,φ)eθ Vφ(r,θ,φ)eφ (11) と表されるとする また, 積分経路として 高次元超球の体積の求め方 公開21年2月23日 工学 / 数学 ガンマ関数 / 特殊関数 / 積分 / 超球 / 高次元 この記事では一般 d d 次元超球の体積について,その求め方をご紹介します。 超球の体積の求め方は幾つか知られていますが,ここでは僕が直感的に
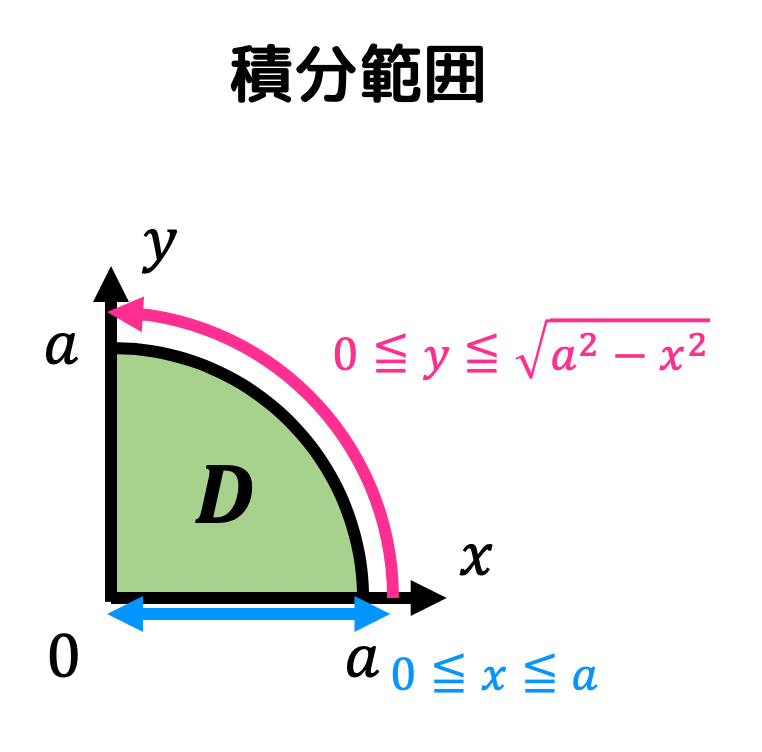
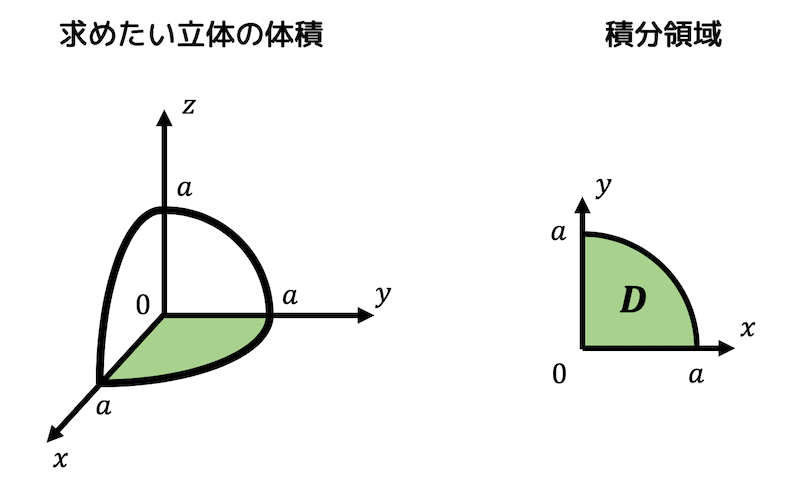
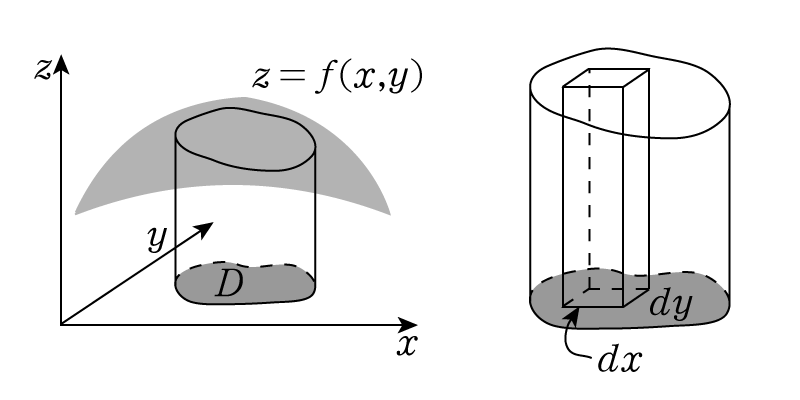
まずは球の式 x 2 y 2 z 2 = a 2 を z = f ( x, y) ≧ 0 の形にしましょう。 すると、 z = f ( x, y) = a 2 − x 2 − y 2 となりますね。 つまり、下の図のような x 軸, y 軸, z 軸の正の部分からなる図形の体積を求めます。 ただし、3つの軸で2等分した図形の体積を求めているので、二重積分で求められる体積の結果は求めたい立体の体積の1/8となります。 なので、球の体積 V は V四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V (x) で表し, x における断面積を S (x) とおきます. 上で復習した面積の求め方と同様にして ⊿V (x)≒S (x)⊿x




球体の体積 積分で求める方法 うちーノート



体積を求める
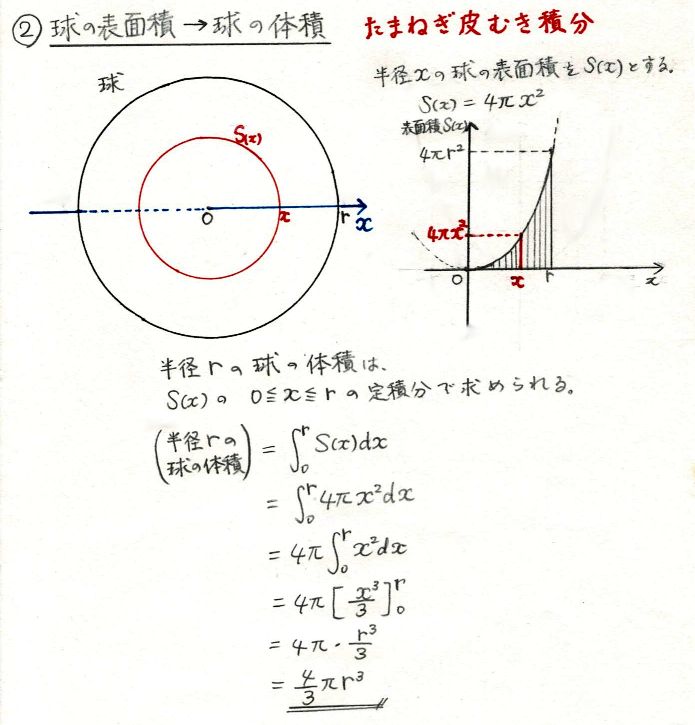
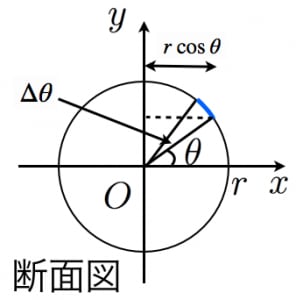
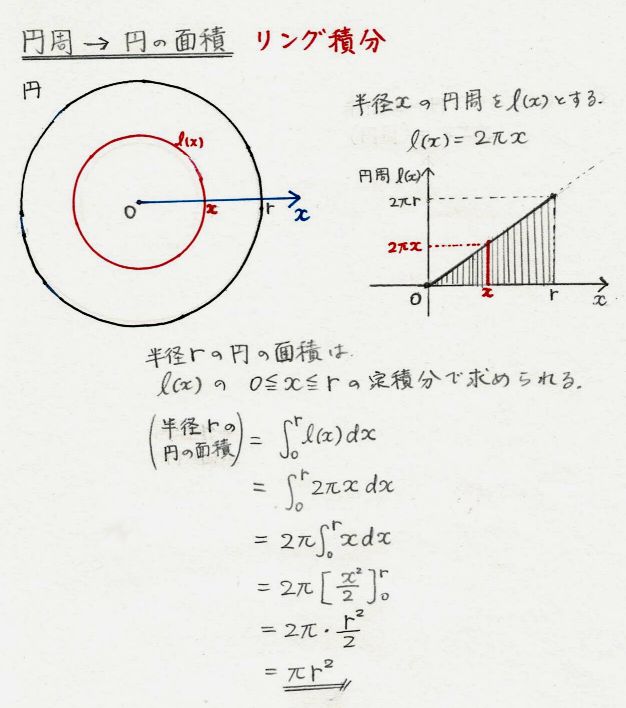
体積は r (半径)を 3 回かけるのがポイントです。 求め方2:球体の体積を用いる方法 求め方1:微小の範囲を考える方法 考え方 青い部分の面積 を考える. 幅は 、長さは なので, より微小な角度を考える 球全体で積分する 計算 求め方2:球の体積を用いる方法 考え方 半径 の球の表面積を とおく. この薄い球殻を集めると球体が完成下のような微分と積分の関係が成り立ちます! くだけた表現をすると、 円周を積分 = 円の面積 球の表面積を積分 = 球の体積 逆に、 円の面積を微分 = 円周 球の体積を微分 = 球の表面積
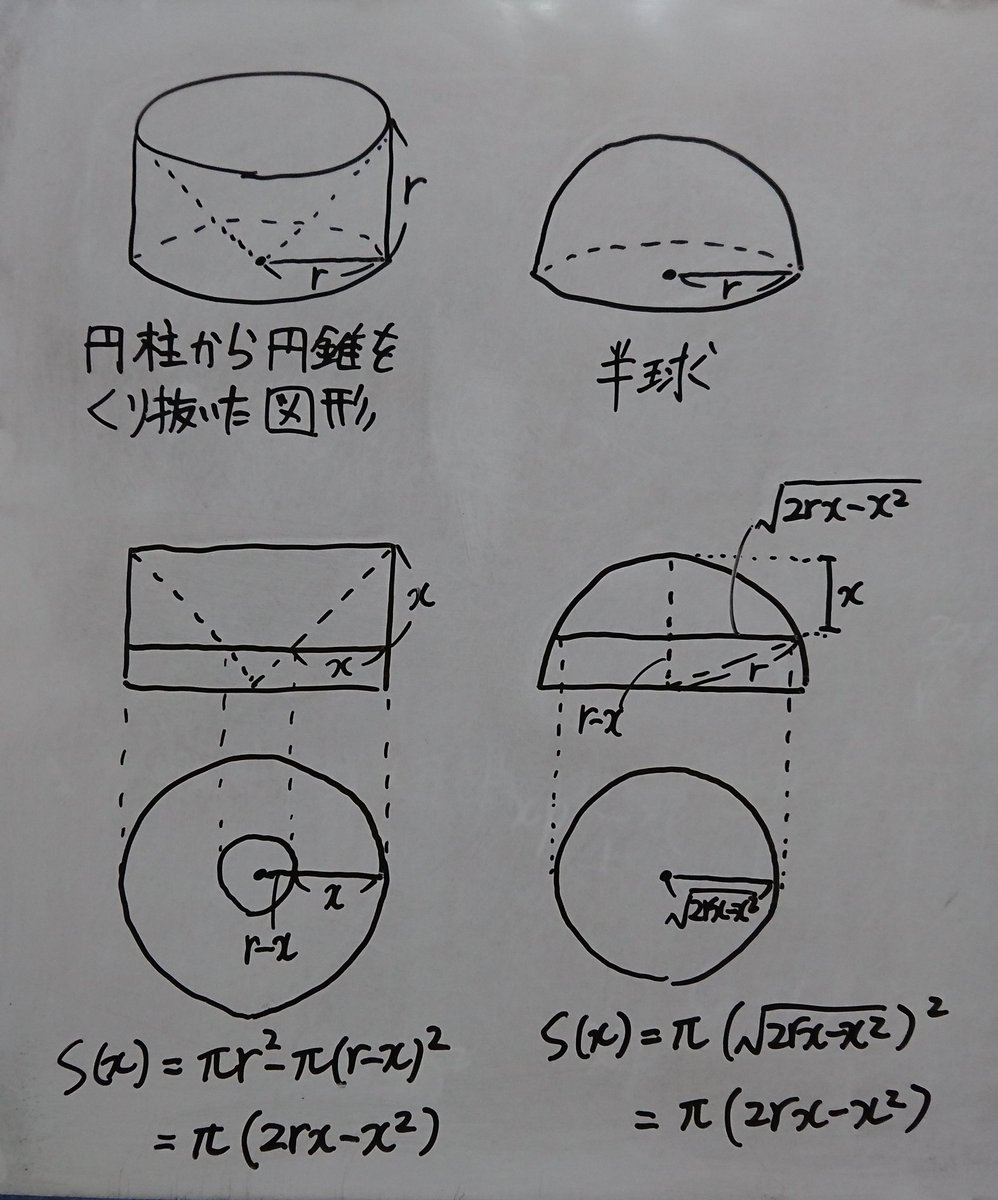



バラノラ 積分を使わずに球の体積 円柱から円錐をくりぬいた図形と半球の各高さにおける断面積が等しいことから球の体積が4 3pr 3だとえいる でも円錐の体積が円柱の体積の1 3と等しいことは仮定しちゃってるから微妙かも



研究
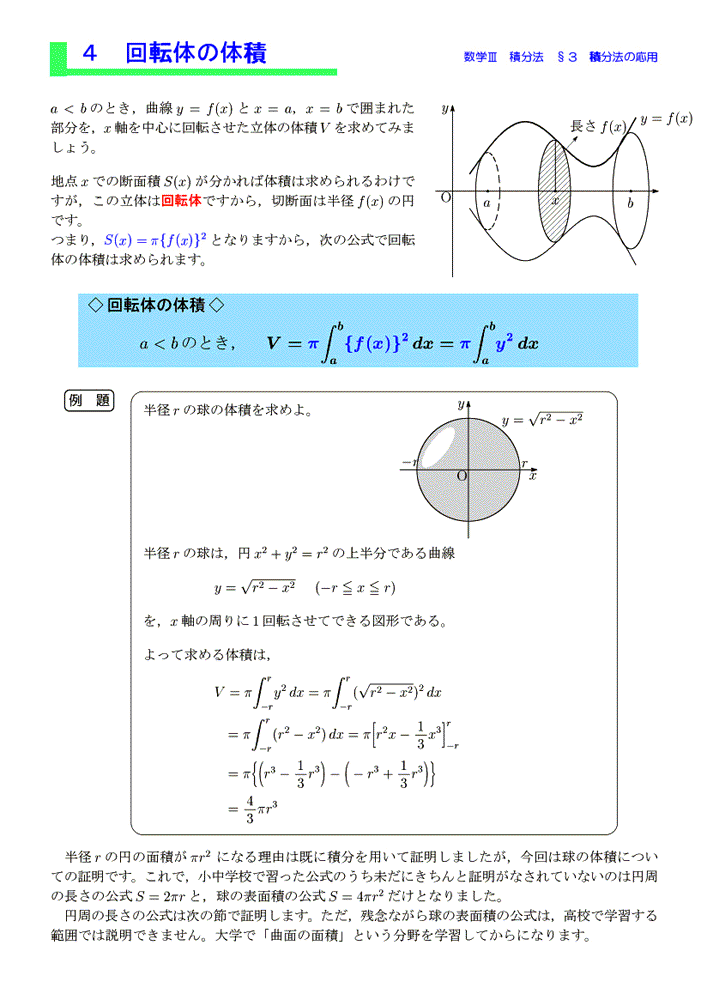
球の体積と表面積 東京大学大学院数理科学研究科・教授 古田幹雄 1 円の面積と円周の長さ 半径rの円の面積はˇr2 です。 グラフv = ˇu2 のu = rにおける接線の傾きを求めてみま す。すると、答えは2ˇrとなります。これは半径rの円周の長さです。つまり、円の面積(球の体積) = (4/3) π r 3 という公式が作られる。 解析的には、高校3年で学ぶ「数学III」の微分積分において、円の回転体の体積として、 球の体積の公式は求められる。(←以前は高校2年で学ぶ「数学II」の内容であった。 x x 軸のまわりに回転させてできる図形の体積は, V = ∫ a b π { f ( x) } 2 d x V=\displaystyle\int_ {a}^b\pi \ {f (x)\}^2dx V = ∫ ab π{f (x)}2dx 例題,証明,および回転体の体積を求める他の公式について。 目次 応用例:球の体積 公式の証明



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の体積と表面積を積分で証明 高校数学の美しい物語
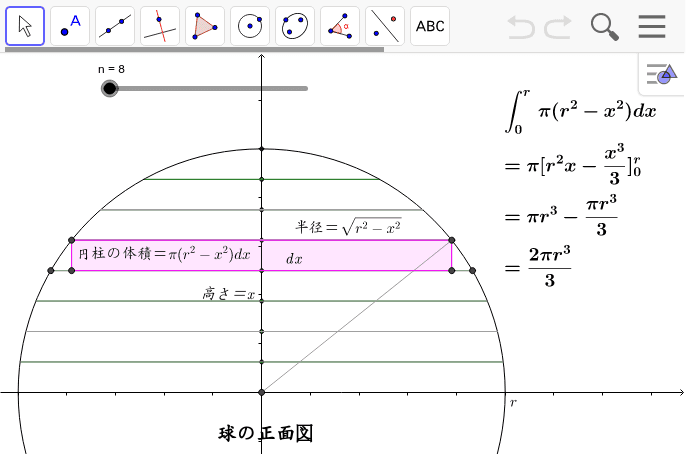
よって、球の体積Vは、円の面積をx 方向に積分すると、V=2∫0rπ(r2-x2) dxより、 V=2πr2x-(x3/3)0r=(4/3)πr3を導くことができる。 ②球の表面積の公式の求め方(1)重積分した2πR 2 (1-d/R)という結果は、上 記で得られた公式より求められる 2πR(R-d) とも一致していますね! 上記では、球冠の側面積を重積分で求めたが、高校の数学Ⅲの範囲で十分求め られ積分計算による体積の求め方!断面積の積分や回転体の体積 球の体積と表面積の公式と覚え方を一目でわかるように図を 小学算数の面積の求め方と公式一覧!四角形・長方形の性質や 面積の求め方 計算公式一覧 Scipursuit



体積を求める



球 体積 求め方 ニスヌーピー 壁紙
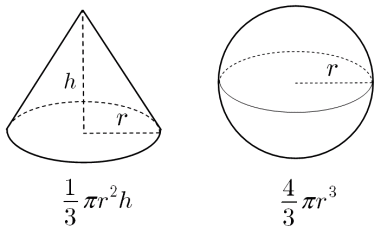
大学数学を使って球の体積を求めるシリーズ(目次)。 今回は3次元球の体積。結果は「球の体積の公式」になります。3次元球の体積3次元球 の体積を求めます。 「極座標のヤコビ行列とヤコビアン : 3次元」より、3次元極座標の体積要素は となるので(積分範囲も注意) まさしく「球の体積まずは円柱の体積の求め方底面積πr^2×高さ2rを援用。 幅 rΔΘ で刻まれた 球の断層 πr^2*cos(Θ) を π/2 から π/2 にかけて積層したイメージ、ないしは 球の断層 πr^2*sin(Θ) を 0 から π にかけて積層したイメージに到達する。回転体の体積の求め方 教材を作成 定積分, 球面, 体積 回転体の体積は積分の公式から簡単に求めることができる。 回転体 線分 回転体東大 回転体の体積 回転体三角形 扇形の回転体 球欠+円錐の体積



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



体積積分 回転体積分 京極一樹の数学塾
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして また、今回積分する範囲は\(r\)から\(r\)までなので、球の体積\(v\)は以下のようになります。 $$V = \int_{R}^{R} π( R^2x^2)dx$$ $$ = π\left R^2 x \frac{ x^3 }{ 3 } \right_{R}^{R}$$ (1B)微小面積(体積)を幾何学的に計算して積分する方法 求めたい面積 S は、変数を x, y とすると、 S = ∫ ∫ d x d y として微小面積について x と y について足し合わせればよい。



数学 球の表面積を積分で計算してもうまくいかない人へ



電気磁気学i Ii 要点 後藤 電気電子システム工学科 中部大学
球1 の半径を r1 r 1 、体積を V 1 V 1 、球2 の半径を r2 r 2 、体積を V 2 V 2 とします。141注1 線積分の引き戻し公式:式() 曲線 上で与えられた線密度 を、 上で積分したもの は で与えられる。 この積分を数直線上の区間 ( ) に引き戻す公式は、以下のようになる: ( ) (あえてルート記号を残しているのは、後述の面積分()や体積積分と合わせるためである。人類はどうやって球の体積を求めたのか 1、アルキメデスは球の体積をどうやって見つけたの? T:球の体積は半径をrとすると、4/3・π・r 3 で求めることができるんです。 覚え方は、『3分で忘れる心配あーるの参上。




球体の表面積 積分で求める方法 うちーノート




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
となり、 球の表面積と体積は微分積分の関係にある ことが理解できます。 もちろん(27)式の\(r\)以外の積分を先にやってしまっても同じ結果が出てきます。ことは普通困難である。大日本図書『数学の世界1』の 考え方と同様な方法で、球の体積から表面積を求め ておいた。 大学の数学、とりわけ微分積分の初期に習う重積分を使って球の表面積と体積の公式を導くことができる。 このブログでは、古典的 な




球の表面積の公式について みたにっき はてな




球の表面積と円の面積 球の表面積や円の面積を積分により求める場合 パラメ Okwave




定積分と面積3 球の表面積 Youtube




球の表面積の公式について みたにっき はてな




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



積分 体積を求める 大人が学び直す数学



球の体積と表面積を積分で証明 高校数学の美しい物語



ベクトルポテンシャル補足 12 での 球の表面積 を求める証明 Jo3krpの独り言




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube




球の体積公式の微分が表面積になっている理由 Youtube



球体の表面積を 積分で求めて下さい 塾で積分を習ったのですが そのとき 球 Yahoo 知恵袋




Mathematics 球の体積と表面積を求める公式 働きアリ



球の体積を重積分で求めたいのですが 上手くいきません は球の上半分 半球 Yahoo 知恵袋



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




球の体積 球の表面積の公式の導出 積分 優技録



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




体積 10 球と円柱の共通部分 怜悧玲瓏 高校数学を天空から俯瞰する




勉強しよう数学 球の表面積を積分で求める



4次元物体の表面積はどうやって計算するのですか Quora




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




4次元の球の体積 テンメイのrun bike




あんじょう勉強 家庭教師のつぶやき




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



1




球の表面積と体積の公式 数学fun



3



Q Tbn And9gcr6jkoybdanugf1fmicpptzy5auleu32fgwe6 X Jkyzlirf8w1 Usqp Cau



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



Juusekibun




球の表面積の求め方 その3 感じる科学 味わう数学




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活




体積の求め方 回転体ではない立体を積分で 数学の偏差値を上げて合格を目指す




高校数学 楕円の面積と回転体の体積 受験の月



大学入試問題



積分を使った球の体積の求め方です 画像のように切って切って Yahoo 知恵袋
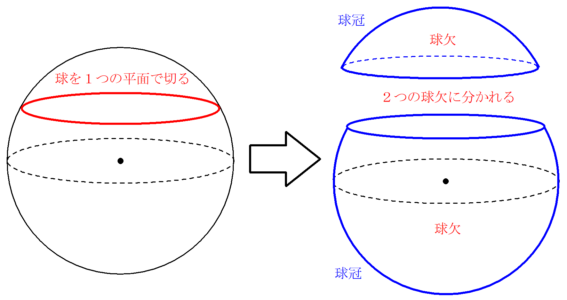



球欠と球冠 Fukusukeの数学めも




球の体積 表面積 無料で使える中学学習プリント



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



質問です 半径aの球について A 球座標系の面積積分から表面積を B Yahoo 知恵袋




回転体の表面積 側面積 身勝手な主張



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




球の表面積 体積 身勝手な主張




球の表面積の求め方 公式と計算例




半球の体積と表面積を計算する 具体例で学ぶ数学




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



1




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



数学 球の表面積を積分で計算してもうまくいかない人へ



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



多重積分の極座標変換 物理の学校




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ




勉強しよう数学 球の表面積を積分で求める




球の体積 球の表面積の公式の導出 積分 優技録



体積を求める



Sphere 01



球の体積の積分 Geogebra




球に関する公式 理数系無料オンライン学習 Kori
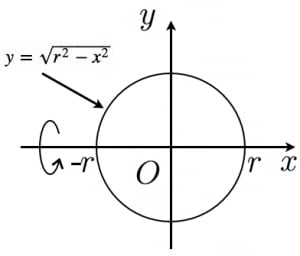



球の体積と表面積を積分で証明 高校数学の美しい物語



球の表面積の公式の求め方




円の面積 球の体積公式の証明 理系ノート




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ




球の表面積を重積分を使って計算してみた Youtube




勉強しよう数学 球の体積を積分で求める




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




初等幾何 球の表面積を求める 大人が学び直す数学



例題対比 球の体積と表面積



球帯と球冠




球体の体積 積分で求める方法 うちーノート




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



数学 球の表面積を積分で計算してもうまくいかない人へ



球の表面積の公式の求め方




球対称な物体による万有引力 高校物理の備忘録



体積と積分 Geogebra



研究




電磁場 Sp




数学講師必見 中学数学でも必須 球の体積 表面積の覚え方と導出まとめ 高校数学 塾講師ステーション情報局




数 積分 積分で球の体積を求めてみる Youtube




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



数学 球の表面積を積分で計算してもうまくいかない人へ




球の表面積と体積の公式 数学fun



数学 球の表面積を積分で計算してもうまくいかない人へ



球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要




球の体積と表面積 公式と計算問題と証明 Irohabook




球の表面積と体積の公式 数学fun




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張


