求積公式(平面) 求積公式(平面) A=面積 正方形 長方形 平行四辺形 備考 a寸法はb辺に対し直角に測ったもの 直角三角形 A=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、 扇形の「弧の長さの求め方」がよくわからない! "扇形の弧の長さと面積"の公式とその証明です! 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明 扇形の公式にあてはめると s = 3×3×π×90/360 = 9π/4 となります。 扇形の公式は覚える必要がない おうぎ形の公式は、ぱっとみるとちょっと長いと思いませんか? 実はこの公式、なぜこの式になるのかさえわかっていれば、覚える必要はありません。

円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張
扇形 弧の長さ 公式 高校
扇形 弧の長さ 公式 高校-扇(おうぎ)形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形を 中学数学 扇形の弧の長さと弦の長さを求める公式をおしえてください。 円の面積を求める公式についてなぜ円の面積は半径×半径×3なのかを小学生に簡単に文で伝えるにはなんと言えば良いでしょうか?




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
扇形とは? 面積・中心角・半径・弧の長さの公式と求め方 21年2月19日 この記事では「扇形(おうぎ形)」について、面積の公式や半径・中心角、この長さの求め方をできるだけ簡単に解説していきます。 また、弧度法(ラジアン)で解く計算問題などもしくは、単純に、1ラジアンの円弧の長さ(=半径(r))の θ倍であるため ・扇形の面積は (r 2 θ)/2 扇形の面積の公式:円弧×半径/2 に代入 もしくは、円全体の面積 πr 2 に割合 θ/2π を掛ければ求弧の長さと面積の公式 <証明> 弧の長さと面積の公式の証明をしておきます。 証明が必要ない方は、次の章へ進んでください。 扇形の弧の長さ 扇形の弧の長さは中心角の大きさに比例する。 中心角が2倍になれば、弧の長さも2倍になる。
扇形の中心角をx°、弧の長さをL、半径をrとすると、 x = 180L/πr になるってやつさ。 つまり、 扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができる んだ。 たとえば、 半径 4 cm、弧の長さが 6π cmの扇形があったとしよう。扇形的弧長與面積 扇形的弧長與面積 1弧長扇形的弧長我們要怎麼求得呢 2扇形面積 這樣以後題目給我們半徑r,跟角度要我們求扇形的弧長或面積,我們就可以輕鬆的套公式把它算出來了 2分でわかる!扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね?? それじゃあ、 扇形の弧の長さの公式 をみていこう! 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。
求扇形弧長與面積。知道以下三個比相等:(1)圓心角:360;(2)扇形弧長:圓周長;(3)扇形面積:圓面積,但應用問題只處理用(1)求弧長或面積。 學習表現: sⅢ2 認識圓周率的意義,理解圓面積、圓周長、扇形面積與弧長之計算方式。 議 題:扇形の弧の長さ( l ength) 公式の導き方 扇形は円の一部分を切り取った図形です。扇形の面積は、「半径が等しい扇形の面積は、中心角に比例する」という性質を使って、円の面積 $\pi r^2$ に$ \frac{\text{中心角}}{360^\circ} $の割合をかけることで求められます。扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。




ラブリー扇形 弧の長さ 公式 最高のカラーリングのアイデア




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
扇形の中心角を求める方程式を利用 半径が3㎝、弧の長さが3 ㎝の扇形の中心角を求めなさい。 まずは、方程式を使って扇形を求める方法について解説していきます。 求めたい中心角を とおいて、方程式を作っていきます。 中心角を とすると、問題N 表示的是扇形角的度数, r 表示半径。 所以当我们要求扇形的面积时,我们肯定要知道这两个未知数 n , r 到底是多少,然后才能带去这个公式去计算;另一种方式求扇形的面积是 S = 1/2lR 这里 l 表示的是所求这个扇形的弧长, r 依旧为扇形所在圆的半径。 扇形の弧の長さや面積を求めることには慣れている人でも え、半径!? どうやって求めるの? と、なってしまうことが多いです。 いざというときに困ってしまわないよう、半径を求める練習をしておきましょう。




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




扇形面積 ラジアン 円の面積 円周 球の體積 表面積の公式の覚え方 微 Eoisg
C 扇形弧長S=rθ d 扇形面積A=1 2 r2θ=1 2 rS (2)三角函數的定義 正弦函數sinA=∠ 的對邊 斜邊 餘弦函數cosA=∠ 的鄰邊 斜邊 正切函數tanA=∠ 的對邊 ∠ 的鄰邊 餘切函數cotA=∠ 的鄰邊 ∠ 的對邊 正割函數secA= 斜邊 ∠ 的鄰邊 餘割函數cscA= 斜邊 ∠ 的對邊 (3)三角函數教學目標 1、能理解圓形、弦、弧、弓形、扇形的意義。 2、能計算扇形的弧長與面積。 能力指標 8s01 能認識生活中的平面圖形 (圓形) 8s 能理解與圓相關的概念(如半徑、弦、弧、弓形等)的意義。 8s21 能理解弧長的公式以及扇形面積的公式。扇形弧長公式扇形圓周長公式精采文章扇形圓周長公式,橢圓形圓周長公式,正方形周長公式,周長計算公式網路當紅,長方形面積公式,扇形面積公式 1/2(r)^2Θ 弧長公式 r Θ (Θ為角度) 參考資料: 我自已 1 001 意見者: MrNatural ( 初學者 2 級 ) 發表時間: 0145 檢舉 ~老人家 ,弧長公式n是



1




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月
と扇形の弧の長さrθ の比が1となる、つまりlim θ!0 sinθ θ = 1 と同値なわけで ある。 rθ rsin θ 2 rsin θ 2 θ 2 θ 2 r r 極限の公式lim θ!0 sinθ θ = 1 を証明するには、やはり曲線の長さを極限で定 義する必要がある。以下でRiemann 積分の復習をして、円弧の長さを積分影片:例題如何計算扇形的弧長?,數學 > 主題式 > 國小 > 空間與形狀 > 平面圖形 > 六年級圓周長與扇形周長。源自於:均一教育平台 願 每個孩子都成為終身學習者,成就自己的未來。おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 °




扇形の弧の長さの求め方 公式と計算例




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト
弯曲的AB部分为弧arc OE为边心距 三角形AOB为三角区 ED 是拱高 弧长计算公式为: (Central Angle / 180°) •π • r 黄色区域为扇形 扇形面积公式为: (Angle AOB / 360°) •π • r² 绿色面积为拱高面积 此面积大小=扇形面积- AOB三角形弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソンNo003 扇形の面積と円弧の長さ 扇形の面積 A m 2 扇形の角度 θ ° 扇の半径 r m 扇形の面積 A m 2 扇形の角度 θ rad 扇の半径 r m 円弧の長さ l m 扇形の角度 θ ° 扇の半径 r m
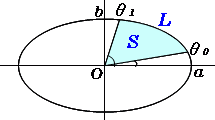



楕円扇形の面積 高精度計算サイト




O Xrhsths 数学 Ii Sto Twitter 第1節 三角関数 角の拡張 D 弧度法と扇形 画像右 例題 半径4 中心角pの扇形の 弧の長さℓと面積sを求めよ
弓形 (緑)は、割線/弦 (破線)と弧 (緑の領域の天井)で囲まれる 扇形の高さ=半径 R は、弦からの高さ h と深さ d の和 円の 半径 を R, 中心角は θ rad = α ° とし、弦の 長さ c および 弧長 s と 矢 の長さ h および扇形の三角形部分の高さを d とする。 扇形のまわりの長さは、 扇形の弧の長さ+半径×2 で求められます。 この扇形の弧の長さ=18×314× 1 ° 360 ° =14(cm) よって、求める扇形のまわりの長さは 14+9×2=3684(cm) 答え 3684㎝ ~平面図形の面積・まわりの長さを求める公式まとめ弧长=半径×圆心角弧度数 (请一定要注意这里是使用的 弧度制 不是圆心角,角度数) 弧长=圆周率× 圆心角 角度×半径/180° 圆心角角度=180°×弧长/(半径×圆周率) 半径=180°×弧长/(圆周率×圆心角角度




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook
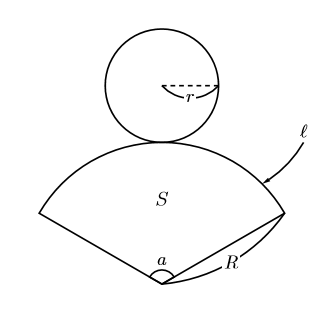



中学数学 円錐関連の公式の導出 数樂管理人のブログ
扇形弧長公式2 最新資源 中一︰棱柱的總表面面積三角棱柱 的複本; 弧度法を使ったおうぎ形の弧の長さと面積 半径が r r で、中心角が θ θ のおうぎ形の弧の長さを l l とし、面積を S S とすると、次が成り立つ。 l = rθ S = 1 2r2θ = 1 2rl l扇形弧長公式3 最新資源 Brown's Ellipsograph;
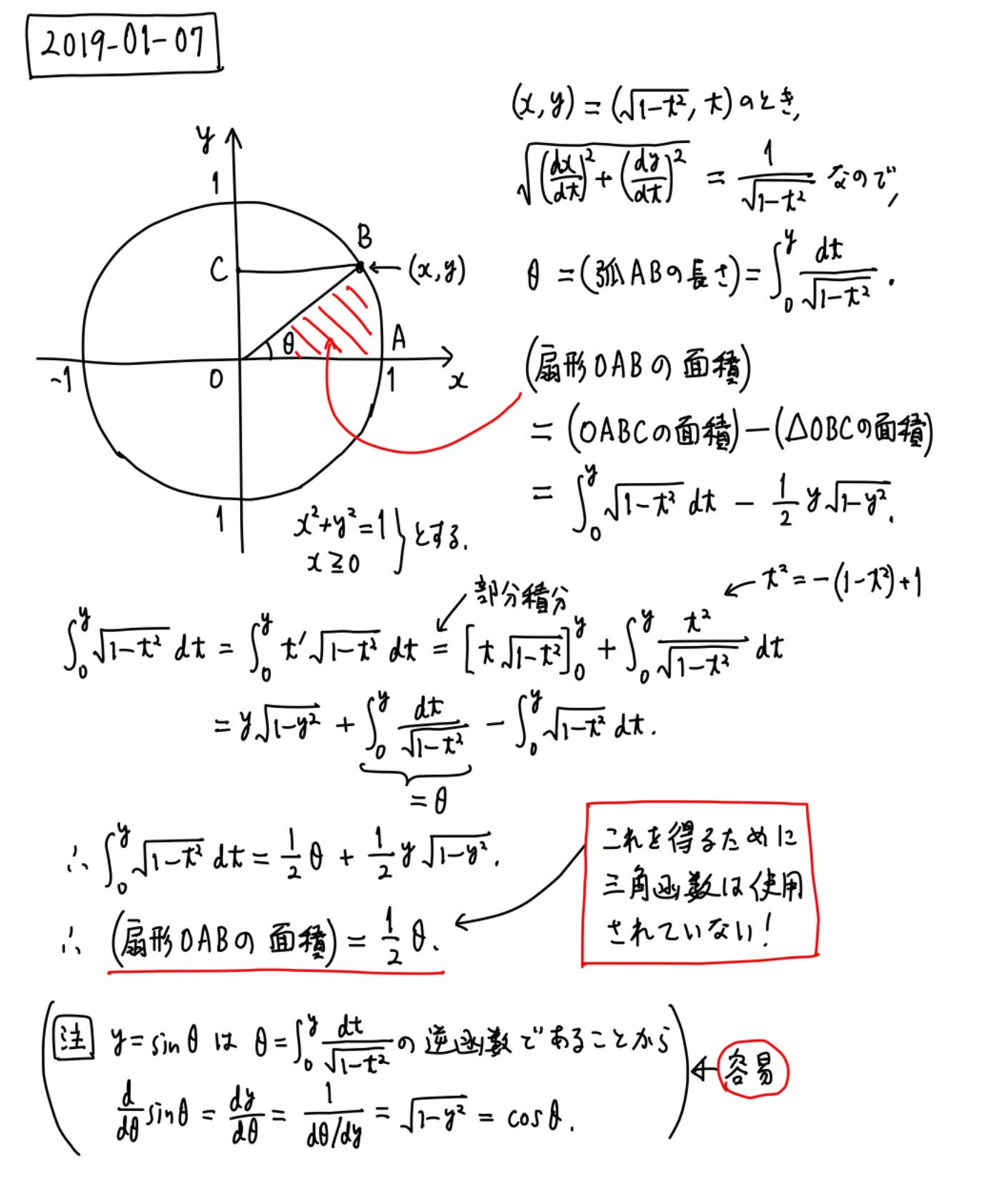



Uzivatel 黒木玄 Gen Kuroki Na Twitteru 数楽 訂正 誤 扇形oabc 正 扇形oab ポイント1 角度 弧 Abの長さをdt 1 T の積分で表示 ポイント2 扇形の面積を 1 T Dtの積分で表示 ポイント3 それらが部分積分で繋がる 訂正版解説画像 T




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
扇形的弧長與面積公式: 若圓半徑為 r,扇形 COD 的圓心角 ∠COD=θ(弧度),2π, ≤ θ 0 ≤ 如下圖所示,令扇形的弧長為 s,面積為 A,則: 円 扇形 の面積 周や弧の長さの公式 数学fun




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく



扇形の弧の長さと面積 時習館 ゼミナール 高等部



中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張
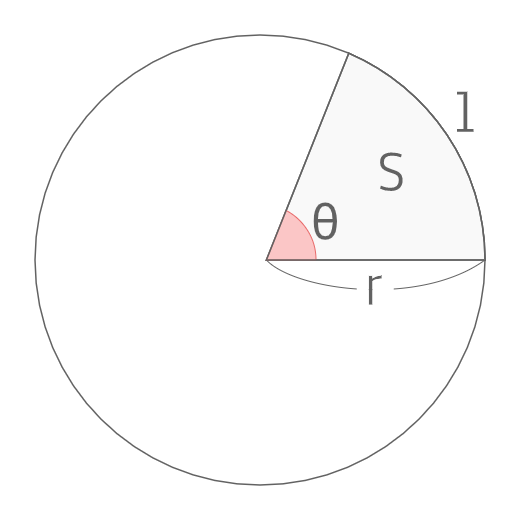



高校数学 扇形の弧の長さと面積 の公式とその証明 Enggy




扇形の中心角の求め方を教えてください Clear




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
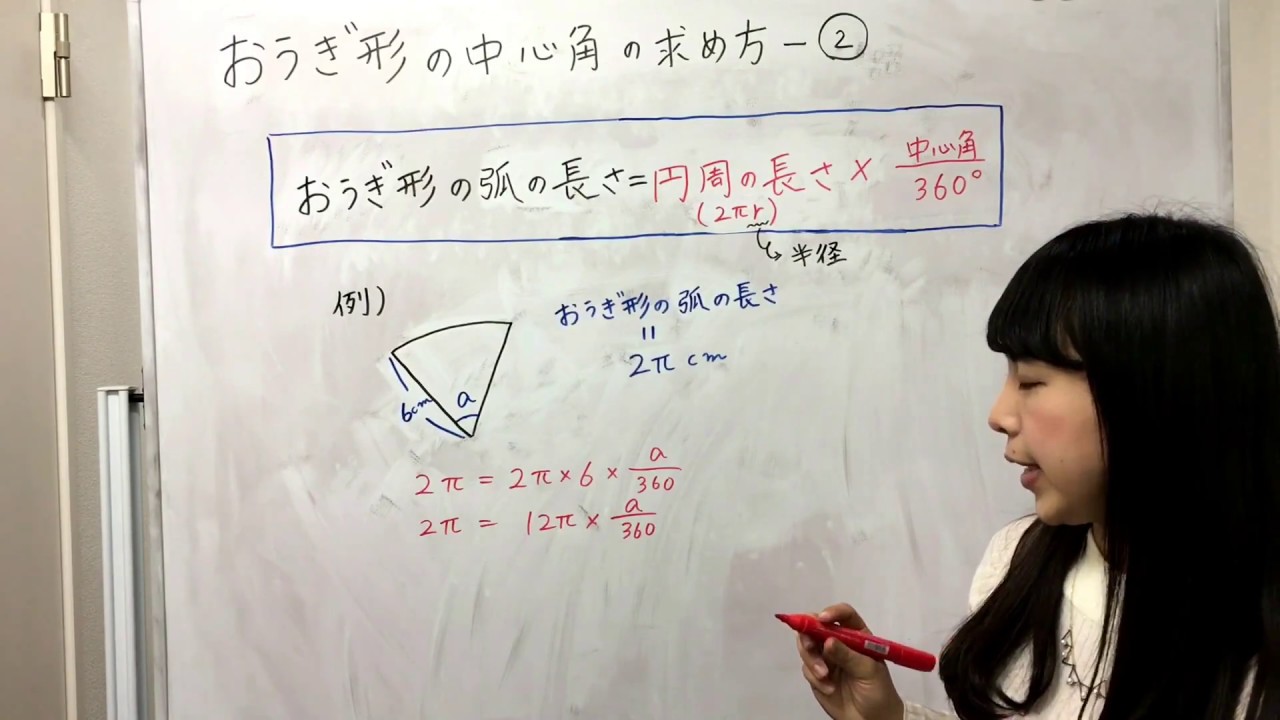



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
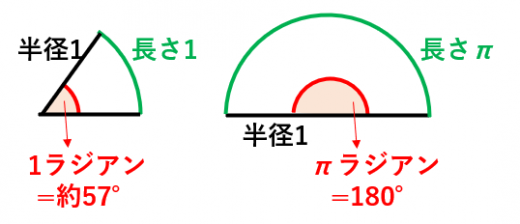



弧度法の意味と度数法に対するメリット 高校数学の美しい物語
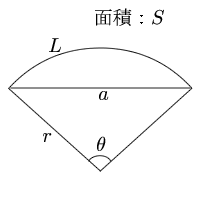



扇形 面積の計算 計算サイト




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




公式を図解 すい体の体積 円すいの表面積の求め方




扇形の弧の長さと面積 計算ドリル 問題集 数学fun




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の面積 ぜひ 弧の長さ を使ってみて 15 Do Your Best Haruka Saki
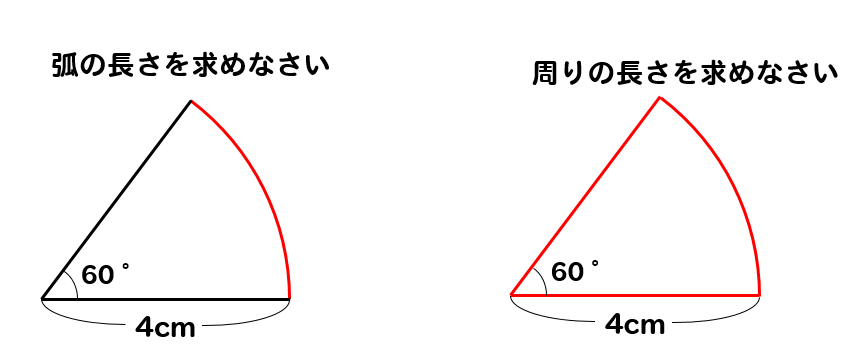



おうぎ形 注意 周りの長さを求める公式を解説 数スタ




扇形の弧の長さの求め方 公式と計算例
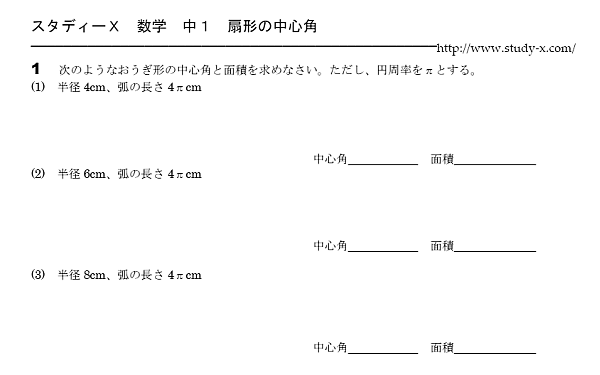



中1 数学 無料学習プリント教材




円弧面積の計算式



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
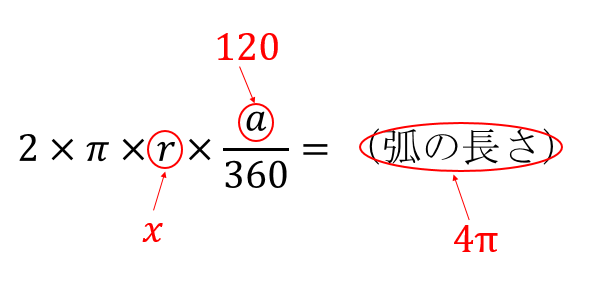



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
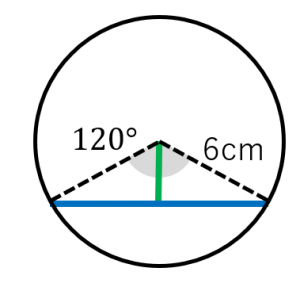



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学
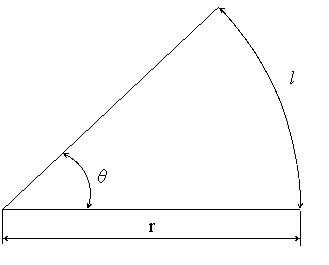



数学の公式集 No 003 幾何図形 扇形の面積と円弧の長さ




円の周りの長さを計算しよう 家庭学習レシピ
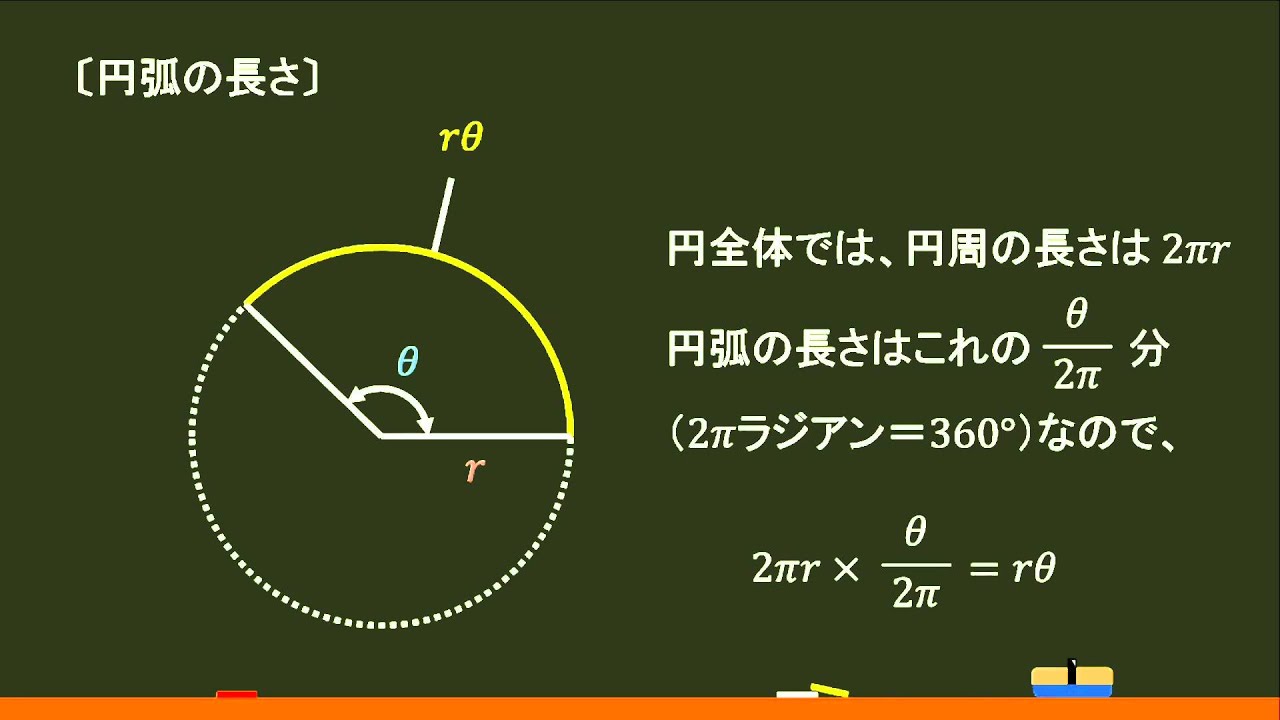



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube




扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube
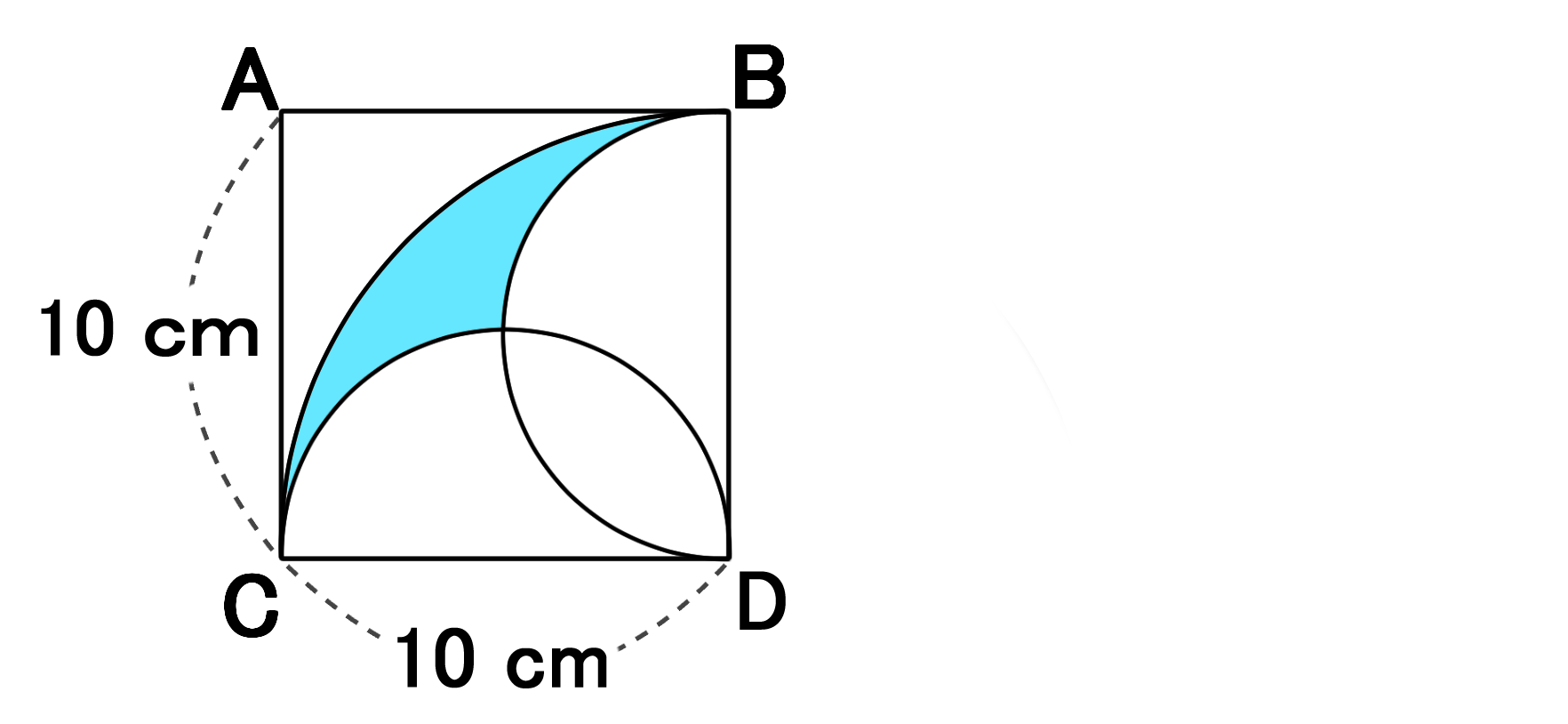



バカでもわかる 中学数学




標準 おうぎ形と正方形の面積 なかけんの数学ノート




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題
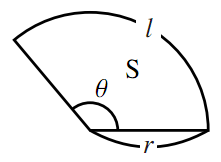



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
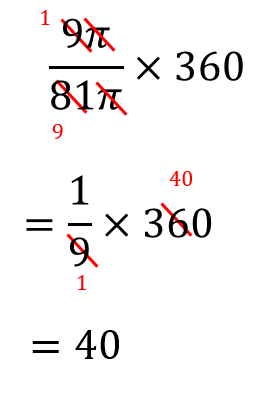



おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




この周の長さが12p 12 Cm なのですが分からないので解き方を教えてください Clear



3



扇形と円 中学から数学だいすき




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の面積 弧の長さ 計算機 かんたん計算機




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw



1



無料 中1数学 標準問題 解答プリント 138 平面図形5 おうぎ形の弧と面積




おうぎ形の弧の長さの公式 算数の公式




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋



扇形の公式 面積 弧の長さ 弦の長さ 数学 エクセルマニア
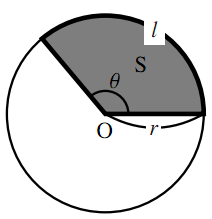



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext
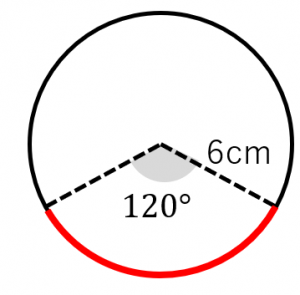



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学
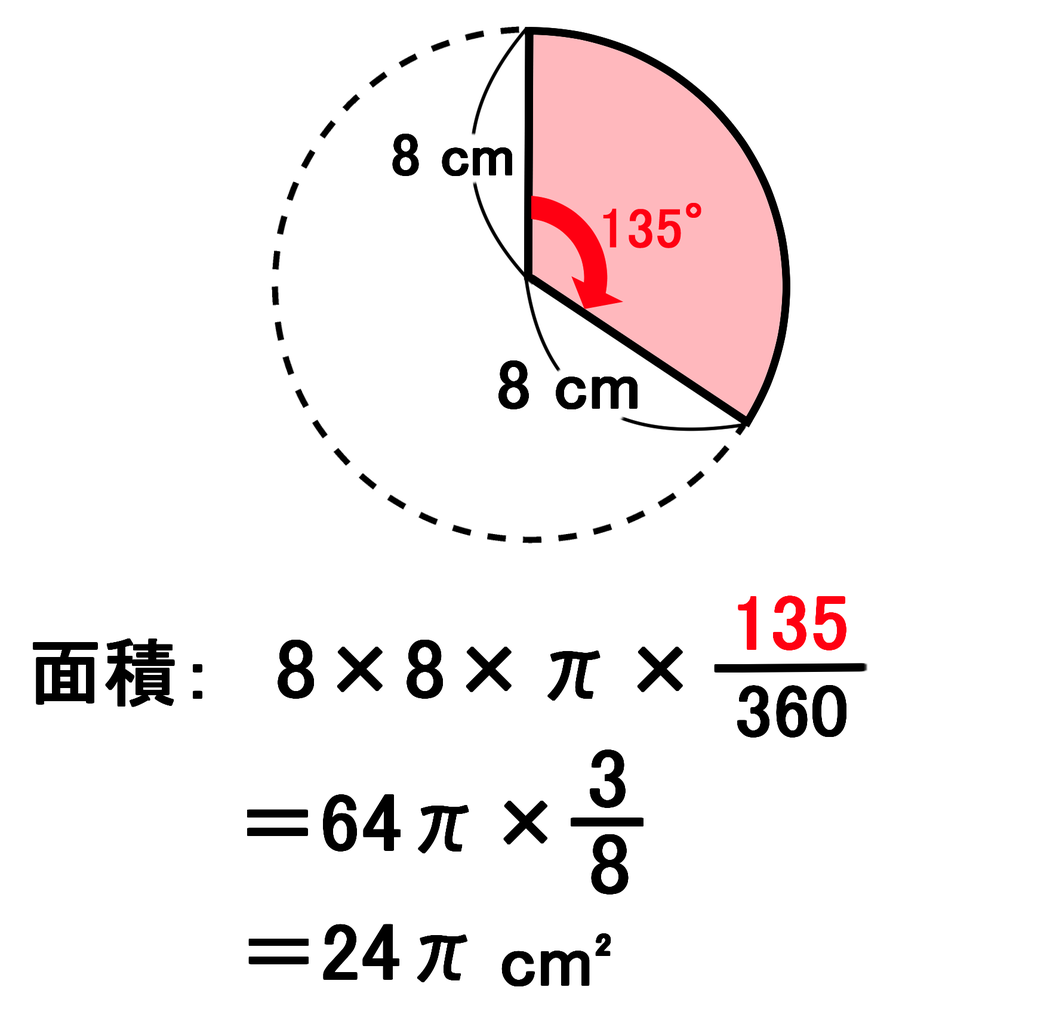



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の面積の求め方 公式と計算例




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




数ii 三角関数弧度法 弧の長さ 扇形の面積 Youtube



3




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




円 扇形 の面積 周や弧の長さの公式 数学fun




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強
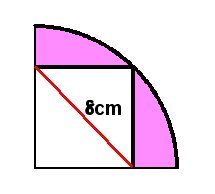



扇形と正方形




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に
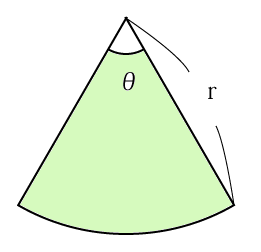



扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




受験数学かずスクール 扇形の弧の長さと面積




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear
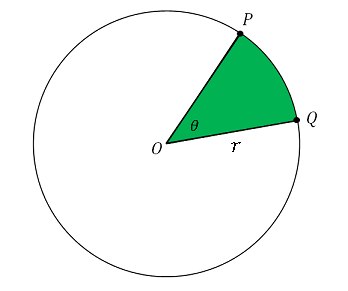



扇形の弧の長さと面積




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




これの表面積の求め方の解説をお願いしたいです W Clear
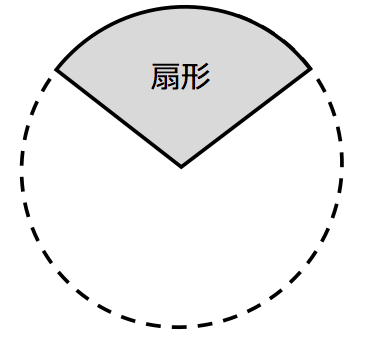



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




弓形の面積 香料ゐっすゐの夢


